In the last few years, the launch of several satellite mega-constellations has been announced, which will place thousands of satellites in the already crowded Low Earth Orbit. In this context, collision avoidance manoeuvres (CAM) are essential to protect both the space environment and the mission of the constellation. However, satellite constellations are usually bound to very tight geometrical constraints, which can be disturbed by these manoeuvres. The aim of this work is to analyse the impact of them on the performance of the constellation, comparing the effect of different manoeuvre strategies.

For this purpose, a generic communications Walker Delta constellation has been defined for the study. More specifically, the constellation chosen was a 67°: 1080/24/12 constellation, located at 600 km altitude. This means that it is composed of a total of 1080 satellites, evenly distributed in 24 orbital planes with a phasing factor of 12, which turns into a 4° phase difference between satellites in adjacent planes. The number of satellites and planes chosen for this constellation also turns into a single redundancy in coverage, meaning that two constellation satellites can be seen from any point on Earth in the latitude range -67° < L < 67°. Additionally, every satellite in the constellation has been assumed to communicate with the other 4 constellation satellites via inter-satellite laser links (ISLLs).

The present study aims to investigate the impact that CAMs have on both the coverage and the ISLL. It is obvious that the region of Earth that can be seen by the satellite (coverage) is affected by the position of the satellite, which will be modified by the manoeuvre. On the other hand, ISLLs require very precise pointing and synchronization between the satellites, which will also be disturbed by the manoeuvres. The main requirements related to the ISLL are associated with the distance between the satellites; the pointing of the beam, defined by two angles: azimuth and elevation; and the slew rate of these angles, which is their rate of change over time.

‍

In order to study different operational situations, six conjunction cases were defined:

• Case 1: One object crossing one orbital plane.
• Case 2: Two objects crossing the same orbital plane.
• Case 3: Two objects crossing two adjacent orbital planes.
• Case 4: One object crossing several orbital planes.
• Case 5: One object orbiting in one of the constellation orbital planes.
• Case 6: Collision cloud in one of the constellation orbital planes.

‍

In order to simulate realistic encounters, Conjuction Data Messages (CDMs) provided by ESA for the Collision Avoidance Challenge ((Kelvins - Collision Avoidance Challenge - Home (esa.int))) were used and modified to fit the geometry of the constellation. The aim of this procedure was to obtain a realistic evolution of the covariances with time.

The different strategies considered for the collision avoidance manoeuvres included two types of manoeuvre: a short term strategy aiming for a specific separation with respect to the second object on the radial direction and a long term strategy aiming for a specific separation on the in-track direction. As the names indicate, the first strategy allows for shorter manoeuvre times, while the second strategy necessitates a smaller orbital change but a longer time. In order to obtain a sensible reduction of the collision probability, 0.2 km was found to be a reasonable separation distance for the radial strategy, and 1 km for the in-track one.

The different CAM strategies simulated included variations of these strategies with regard to the time of the manoeuvre, represented by the time difference between manoeuvre and the time of closest approach (TCA) [katex] \Delta t_{m-tca} [/katex], and the number of orbital revolutions used to come back to the nominal orbit after the manoeuvre [katex]n_{ph}[/katex].
The simulations intended to recreate the operational situation as accurately as possible. Since the goal of each simulation is to study the impact of a specific manoeuvre strategy, the parameters defining the CAM strategy are established beforehand. At the beginning of the simulation the encounter is created and the first CDM is received. The time at which the satellite will manoeuvre is derived from the TCA of the encounter and the parameters of the CAM. The satellite keeps receiving CDMs, thus following up the encounter, until the time of the manoeuvre is reached. Then, if the collision probability is above the threshold of 10e-4, the manoeuvre is performed. The operator keeps receiving CDMs so the collision probability is verified to be low enough. After the time of closest approach has passed, a second manoeuvre is performed in order to take the satellite back to its nominal position.

The results shown here correspond to Case 1 and are used to asses the impact of manoeuvring a single constellation satellite. The first comparison is done between the radial and the in-track strategies. The figures below show the variations in the geometry between the manoeuvred satellite and the next in the same orbital plane in the direction of the movement. More specifically, it shows the variations in the distance, elevation and azimuth with respect to the nominal case. The slew rates are not shown here for simplicity. It is important to note that, due to the geometry of the encounter, the first strategy resulted on the manoeuvred satellite moving to an orbit lower than the nominal one, while the second one took the satellite to an orbit higher than nominal. As a consequence, the variations of the geometry evolve in opposite directions for the two strategies. Anyhow, it is easily observable that the variations due to the radial strategy have a much bigger magnitude than the ones due to the in-track strategy. It is also easy to note that the variations in the azimuth are significantly smaller than the variations of the other parameters. This was already expected, since the manoeuvre strategies do not change the orbital plane of the satellite, only its altitude.

‍

‍

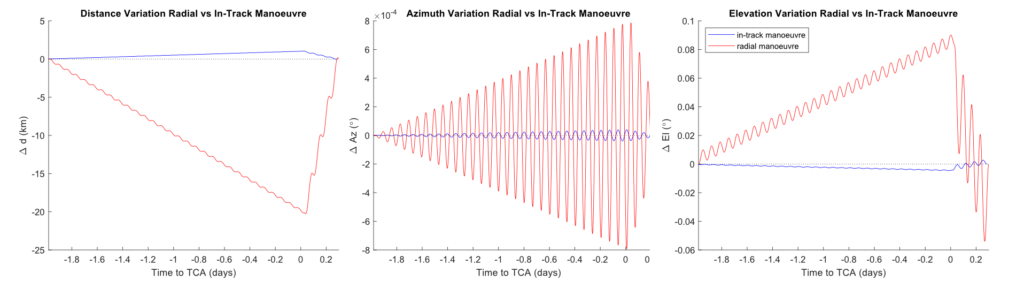
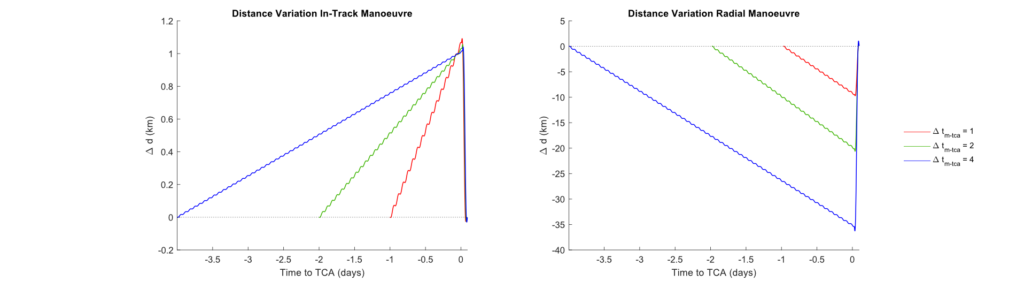
When comparing the impact of different manoeuvre times, the effect of varying [katex] \Delta t_{m-tca} [/katex] changes with the two strategies. The magnitude of the orbital change for the radial strategy only depends on the aimed miss distance. Therefore, the deviations from the nominal case keep growing with time at a constant rate, giving rise to much bigger deviations, the earlier the manoeuvre is performed. In the case of the in-track strategy, an earlier manoeuvre turns into a smaller orbital change needed, giving rise to very similar deviations at the TCA. For simplicity, only the graphs corresponding to the deviations in the distance will be shown here.

‍

‍

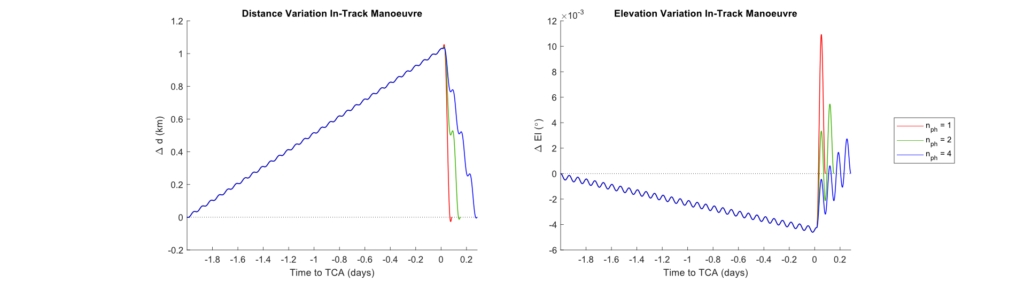
On the other hand, when a lower number of orbits is used to come back to the nominal orbit, the time that the satellite spends in a different orbit is smaller, but the orbital change needed for the second transit orbit is bigger, which can give rise to peaks in the deviations. These peaks are not significant on the distance, but can become problematic on the elevation. The following two figures show these deviations in both distance and elevation for the in-track manoeuvre. It is also important to note that the values used for [katex] n_{ph} [/katex] in a typical operational case would probably be higher, and therefore not that problematic.

‍

‍

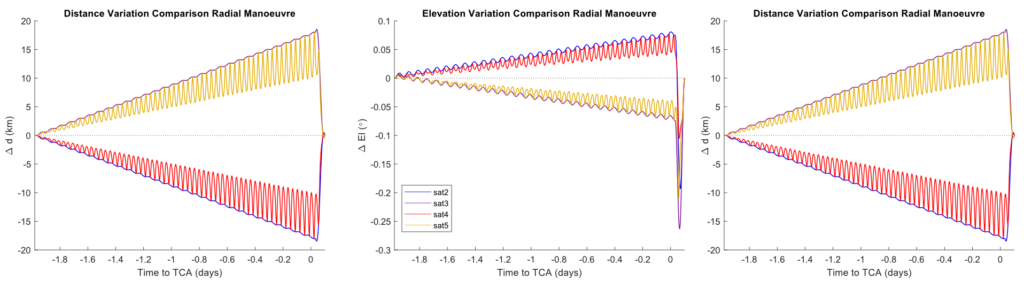
The same simulations were performed in order to compare these effects for the 4 satellites that are linked to the manoeuvred one. It is important to note that, in order to save computational time, all perturbations were turned off on the propagator for these simulations.

‍

‍

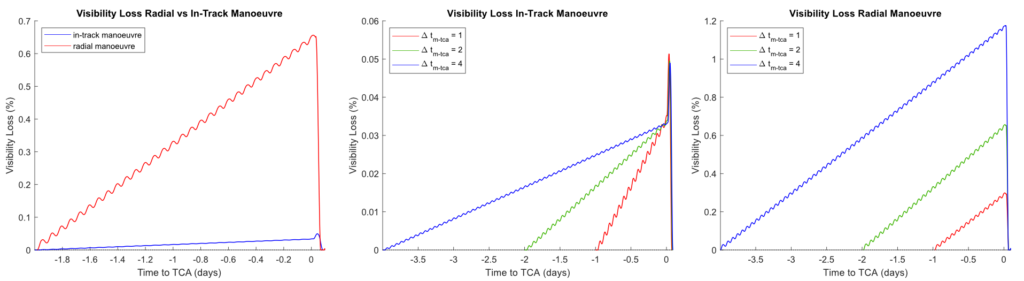
In order to compute the variations on the coverage, the visibility loss (%) has been defined as the area that is seen from the nominal position that is not seen from the manoeuvred one, divided by the total area seen from the nominal position to normalize the value, and multiplied by 100 to obtain a percentage. As can be expected from the previous results, the visibility loss is remarkably larger for the radial case. Also, for the radial strategy an earlier manoeuvre turns into a big increase on the visibility loss, while for the in-track manoeuvre the visibility loss at TCA is very similar for all manoeuvre times. However, the total visibility loss for the whole duration of the manoeuvre would still be bigger for early manoeuvres, since the loss is more extended in time. This can be seen in the following figures.

‍

‍

When examining Case 2, thus two objects crossing the same orbital plane, two contiguous satellites were assumed to undergo the encounters, in order to get the maximum impact. The results proved that the impact of this situation strongly depends on the strategy chosen to manoeuvre both satellites. If both satellites move to a higher orbit, the effects of the manoeuvres "compensate" each other. As a result, both satellites will undergo an impact equivalent to Case 1 with respect to the non-manoeuvred satellites, and smaller deviations in the geometry between them. On the other hand, if one of the satellites is manoeuvred to a higher orbit and the other one to a lower one, the effects of both manoeuvres add up, which can give rise to problematic situations.

For the Case 3, two objects crossing adjacent orbital planes, contiguous satellites (but in adjacent planes) were chosen as well in order to maximize the impact. The conclusion was the same as for Case 2: if the manoeuvres are performed in the same direction the effects compensate each other, but if they are carried out in opposite directions they add up. This result shows the importance of taking into account all the constellation satellites when a manoeuvre is performed.

When examining Case 4, one object crossing several orbital planes, the most problematic situation corresponded to objects with the same orbital period as the constellation satellites, which would encounter the same object over and over again until the differential perturbations move them apart. Different strategies were proposed for this case, being the most promising one to perform a manoeuvre and to come back to the nominal altitude, but not to the nominal position. Thus, not adjusting the phasing. This way, The deviations from the nominal position do not keep building up, staying constant in values similar to the ones analysed before. The phasing can be re-adjusted once the external object has moved far enough from the nominal position of the constellation satellite.

Case 5 examines the situation in which an object orbits in one of the constellation planes. The most extreme case would occur when, additionally, the orbit of the object is also circular and at the same altitude of the constellation satellites. In the case in which the object orbits in the same direction as the constellation, it would not be problematic for the objects orbiting in the same plane, but could generate problems similar to the one described for Case 4 to the satellites in other constellation planes. The same strategies as before would be recommended. If the satellite is orbiting in the direction opposite to the constellation satellites, it would lead to an unbearable number of encounters in a very short period of time. Probably the most reasonable strategy would be to move all the satellites in that orbital plane to a different orbit. The possibility of moving as well the other satellites of the constellation in order to maintain the geometry should also be further studied.

For Case 6, a fragmentation was simulated at the altitude of the constellation, and the encounters closer than 1 km in any direction during the week after the fragmentation were computed. When assumed that long-term strategies were used when possible, numerous encounters leading to problematic situations such as the ones shown in Case 2 and Case 3 were found. On the other hand, reducing the time used for the manoeuvre reduced the number of problematic encounters in almost a 70%. Even when a much deeper study is needed in this aspect, this result already shows an example on the benefits that short-term manoeuvres can have in some specific operational cases. It is also important to note that, the fact that two contiguous satellites need to manoeuvre, does not have to be a disadvantage if both manoeuvres are performed in the same direction. Therefore, the most important conclusion is that all these encounters would need to be examined closely and the manoeuvres coordinated, giving rise to a very high operational complexity. Additionally, a problem that could not be represented here is the time delay between the fragmentation and the time that it takes to track the fragments. Thus, for many of the risky encounters found it would not even be possible to perform a manoeuvre.

To conclude, the impact of different CAM strategies has been compared, showing the benefits and disadvantages of each of them. In turn, the final CAM strategy will always be a trade-off. The importance of a proper manoeuvre design in order to avoid unnecessary harmful impacts has been demonstrated. It has also been shown that the whole constellation needs to be taken into account when any manoeuvre is being planned. Additionally, these manoeuvres should be considered from the design stages in order to include both additional fuel budget and enough flexibility on the geometrical constraints.

‍

The article was written by Lucía Ayala Fernández. ‍

Lucía spent 6 months at OKAPI:Orbits at the end of her dual degree Spacemaster program at Lulea University and University Paul Sabatier Toulouse. During this time, she worked on analyzing the impact of collision avoidance manoeuvres on the service delivery of large satellite constellation. This article is a summary of the resulting Master's thesis.